Search results

Triangular Element for Plate Bending - Part 2

Summary

Describes strain and stress calculation for a simple triangular element for thin plate bending.

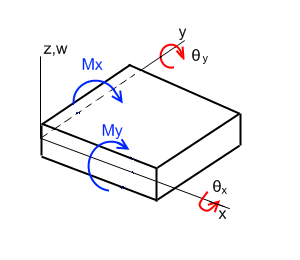
Strain, Stress and Moment

Continue from Part 1, we can now define strains as

{ε} =    ∂2w/∂x2  ∂2w/∂y2 2∂2w/∂x∂y Remember from Area Coordinates that L1 L2 L3 = a1 a2 a3 b1 b2 b3 c1 c2 c3 1 x y

Let
        L_cy2 = ∂²(½L₁L₂L₃)/∂y² = c₁c₂L₃ + c₁L₂c₃ + L₁c₂c₃

   ∂²w/∂y² = β₄(2c₁c₁L₂ + 4L₁c₁c₂ + L_cy2) + β₅(2c₁c₁L₃ + 4L₁c₁c₃ + L_cy2)
               + β₆(2c₂c₂L₃ + 4L₂c₂c₃ + L_cy2) + β₇(2c₂c₂L₁ + 4L₂c₂c₁ + L_cy2)
               + β₈(2c₃c₃L₁ + 4L₃c₃c₁ + L_cy2) + β₉(2c₃c₃L₂ + 4L₃c₃c₂ + L_cy2)

Similarly, let

       L_cx2 = ∂²(½L₁L₂L₃)/∂x² = b₁b₂L₃ + b₁L₂b₃ + L₁b₂b₃

   ∂²w/∂x² = β₄(2b₁b₁L₂ + 4L₁b₁b₂ + L_cx2) + β₅(2b₁b₁L₃ + 4L₁b₁b₃ + L_cx2)
               + β₆(2b₂b₂L₃ + 4L₂b₂b₃ + L_cx2) + β₇(2b₂b₂L₁ + 4L₂b₂b₁ + L_cx2)
               + β₈(2b₃b₃L₁ + 4L₃b₃b₁ + L_cx2) + β₉(2b₃b₃L₂ + 4L₃b₃b₂ + L_cx2)

Let,

   Lcxy = ∂²(½L₁L₂L₃/∂x∂y = ½(b₁c₂L₃ + b₁L₂c₃ + c₁b₂L₃ + L₁b₂c₃ + c₁L₂b₃ + L₁c₂b₃)

   ∂²w/∂x∂y = β₄(2c₁b₁L₂ + 2L₁b₁c₂ + 2L₁c₁b₂ + Lcxy) +
       β₅(2c₁b₁L₃ + 2L₁b₁c₃ + 2L₁c₁b₃ + Lcxy) + β₆(2c₂b₂L₃ + 2L₂b₂c₃ + 2L₂c₂b₃ + Lcxy) +
       β₇(2c₂b₂L₁ + 2L₂b₂c₁ + 2L₂c₂b₁ + Lcxy) + β₈(2c₃b₃L₁ + 2L₃b₃c₁ + 2L₃c₃b₁ + Lcxy) +
       β₉(2c₃b₃L₂ + 2L₃b₃c₂ + 2L₃c₃b₂ + Lcxy)

Putting these into matrix form:

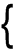ε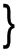

=

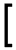0 0 0 XX4 XX5 XX6 XX7 XX8 XX9 0 0 0 YY4 YY5 YY6 YY7 YY8 YY9 0 0 0 XY4 XY5 XY6 XY7 XY8 XY9

CI

d

XX4 = (2b₁b₁L₂ + 4L₁b₁b₂ + L_cx2)
XX5 = (2b₁b₁L₃ + 4L₁b₁b₃ + L_cx2)
XX6 = (2b₂b₂L₃ + 4L₂b₂b₃ + L_cx2)
XX7 = (2b₂b₂L₁ + 4L₂b₂b₁ + L_cx2)
XX8 = (2b₃b₃L₁ + 4L₃b₃b₁ + L_cx2)
XX9 = (2b₃b₃L₂ + 4L₃b₃b₂ + L_cx2)

YY4 = (2c₁c₁L₂ + 4L₁c₁c₂ + L_cy2)
YY5 = (2c₁c₁L₃ + 4L₁c₁c₃ + L_cy2)
YY6 = (2c₂c₂L₃ + 4L₂c₂c₃ + L_cy2)
YY7 = (2c₂c₂L₁ + 4L₂c₂c₁ + L_cy2)
YY8 = (2c₃c₃L₁ + 4L₃c₃c₁ + L_cy2)
YY9 = (2c₃c₃L₂ + 4L₃c₃c₂ + L_cy2)

XY4 = 2(2c₁b₁L₂ + 2L₁b₁c₂ + 2L₁c₁b₂ + Lcxy)
XY5 = 2(2c₁b₁L₃ + 2L₁b₁c₃ + 2L₁c₁b₃ + Lcxy)
XY6 = 2(2c₂b₂L₃ + 2L₂b₂c₃ + 2L₂c₂b₃ + Lcxy)
XY7 = 2(2c₂b₂L₁ + 2L₂b₂c₁ + 2L₂c₂b₁ + Lcxy)
XY8 = 2(2c₃b₃L₁ + 2L₃b₃c₁ + 2L₃c₃b₁ + Lcxy)
XY9 = 2(2c₃b₃L₂ + 2L₃b₃c₂ + 2L₃c₃b₂ + Lcxy)

 Let,
 

ε

=

B

d

B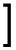

=

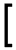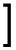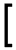0 0 0 XX4 XX5 XX6 XX7 XX8 XX9 0 0 0 YY4 YY5 YY6 YY7 YY8 YY9 0 0 0 XY4 XY5 XY6 XY7 XY8 XY9

CI

Stresses are defined as moment per unit length.

   {M} = [D]{ε} = [D] [B] {d}

Mx My Mxy

=

Et3 12(1-v2)

1   v  0 v   1  0  0   0 (1-v)/2

∂2w/∂x2  ∂2w/∂y2 2∂2w/∂x∂y

Stiffness matrix is then,

   [K] = [D][B]

where,

D

=

Et3 12(1-v2)

1   v  0 v   1  0  0   0 (1-v)/2

Part 1 - Displacement, shape functions