Search results

Triangular Element for Plate Bending - Part 1

Summary

Describes the implementation details of a simple triangular element for thin plate bending

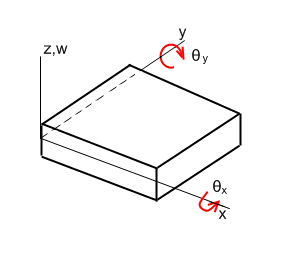
Displacement

For bending of thin plate, we only consider the bending action resulted from forces normal to the plate. In-plane forces are not considered. In this case, the strains and stresses are uniquely described by the vertical displacement, w (assume the plate lies horizontally). w can be expressed with the help of Area Coordinates.

w = β1L1 + β2L2 + β3L3       + β4(L1²L2 + ½L1L2L3) + β5(L1²L3 + ½L1L2L3)       + β6(L2²L3 + ½L1L2L3) + β7(L2²L1 + ½L1L2L3)       + β8(L3²L1 + ½L1L2L3) + β9(L3²L2 + ½L1L2L3) At any point, the displacement vector is {d} =   w θx θy   =     w  ∂w/∂y -∂w/∂x Remember from Area Coordinates that L1 L2 L3 = a1 a2 a3 b1 b2 b3 c1 c2 c3 1 x y

Let
       L_cy = ∂(½L₁L₂L₃)/∂y = ½(c₁L₂L₃ + L₁c₂L₃ + L₁L₂c₃)

   ∂w/∂y = β₁c₁ + β₂c₂ + β₃c₃
            + β₄(2L₁c₁L₂ + L₁²c₂ + L_cy) + β₅(2L₁c₁L₃ + L₁²c₃ + L_cy)
            + β₆(2L₂c₂L₃ + L₂²c₃ + L_cy) + β₇(2L₂c₂L₁ + L₂²c₁ + L_cy)
            + β₈(2L₃c₃L₁ + L₃²c₁ + L_cy) + β₉(2L₃c₃L₂ + L₃²c₂ + L_cy)

Similarly, let

       L_cx = ∂(½L₁L₂L₃)/∂x = ½(b₁L₂L₃ + L₁b₂L₃ + L₁L₂b₃)

   ∂w/∂x = β₁b₁ + β₂b₂ + β₃b₃
            + β₄(2L₁b₁L₂ + L₁²b₂ + L_cx) + β₅(2L₁b₁L₃ + L₁²b₃ + L_cx)
            + β₆(2L₂b₂L₃ + L₂²b₃ + L_cx) + β₇(2L₂b₂L₁ + L₂²b₁ + L_cx)
            + β₈(2L₃b₃L₁ + L₃²b₁ + L_cx) + β₉(2L₃b₃L₂ + L₃²b₂ + L_cx)

Now, let us evaluate displacement vector {d} at each node. The area coordinates,  (L₁,L₂,L₃) at each node are

 P1 = (1, 0, 0)
 P2 = (0, 1, 0)
 P3 = (0, 0, 1)

We immediately conclude that

   L_cy = L_cx = 0 at all nodes

Substitute the values of (L₁,L₂,L₃) into the expressions for w, θ_x, θ_y, we have,

 w₁ = β₁
θ_x1 = (∂w/∂y)₁ =  β₁c₁ + β₂c₂ + β₃c₃ + β₄c₂ + β₅c₃
θ_y1 =-(∂w/∂x)₁ = -β₁b₁ - β₂b₂ - β₃b₃ - β₄b₂ - β₅b₃

 w₂ = β₂
θ_x2 = (∂w/∂y)₂ =  β₁c₁ + β₂c₂ + β₃c₃ + β₆c₃ + β₇c₁
θ_y2 =-(∂w/∂x)₂ = -β₁b₁ - β₂b₂ - β₃b₃ - β₆b₃ - β₇b₁

 w₃ = β₃
θ_x3 = (∂w/∂y)₃ =  β₁c₁ + β₂c₂ + β₃c₃ + β₈c₁ + β₉c₂
θ_y3 =-(∂w/∂x)₃ = -β₁b₁ - β₂b₂ - β₃b₃ - β₈b₁ - β₉b₂

Write this into matrix form,

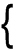w1 θx1 θy1 w2 θx2 θy2 w3 θx3 θy3

=

1 0 0 0 0 0 0 0 0 c1 c2 c3 c2 c3 0 0 0 0 -b1 -b2 -b3 -b2 -b3 0 0 0 0 0 1 0 0 0 0 0 0 0 c1 c2 c3 0 0 c3 c1 0 0 -b1 -b2 -b3 0 0 -b3 -b1 0 0 0 0 1 0 0 0 0 0 0 c1 c2 c3 0 0 0 0 c1 c2 -b1 -b2 -b3 0 0 0 0 -b1 -b2

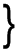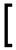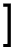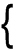β1 β2 β3 β4 β5 β6 β7 β8 β9

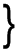or        {d} = [C]{β}

Solve the equations, we have

{β} = [CI] {d}   where [CI] = [C]^-1

Part 2 - Strain, stress and moment