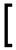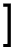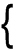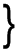Area Coordinates
Summary
Area coordinate is used in the formulation of 2D triangular elements for Finite
Element Analysis. This is often used in plane stress and plate bending analysis.
Definition
In the diagram on the right, we have a
triangle. A point within the triangle, say P, has normal coordinates of (x,y).
However, this is sometimes not convenient. For example, if we want to integrate
over the area, we have to cope with the different boundaries.
Another way to express point P is using the so called Area Coordinates. The area
coordinates of point P are defined as:
P(L1, L2, L3)
where,
L1 = Area of P-2-3 / A
L2 = Area of P-1-2 / A
L3 = Area of P-1-3 / A
In the above, A = area of the triangle.
|
 |
It is now obvious that:
- On line 2-3, L1=0.
- On each line that is parallel to line 1-2, L1 is the same
- The range of L1,L2,L3 is always 0~1.
- The sum of L1,L2,L3 is always 1, that is,
L1 + L2 + L3 = 1
How do we relate (L1,L2,L3) to (x,y) ?
This can be done through the coordinates at the nodes 1,2,3 and by linear
interpolation:
1 = L1 + L2 + L3
x = x1*L1 + x2*L2 + x3*L3
y = y1*L1 + y2*L2 + y3*L3
In matrix form, this can be expresses as:
This can be solved explicitly. However, we shall use a computer function to do the matrix inversion. The result is expressed as:
where,
Inverse Matrix
Inverse matrix can be found using Gauss-Jordan Elimination, in which, we write,
Using row manipulations, we can make the left part a unit matrix (diagonals 1, all rest 0). The right part is then the inverse matrix.
Let's see an example.
(x1,y1) = (-5,0)
(x2,y2) = (5,0)
(x3,y3) = (0,5)
The augmented matrix:
Multiply the 1st row by 5, add to the 2nd row:
|
|  |
Devide the 2nd row by 10 and 3rd row by 5:
Multiply 3rd row by -0.5 and add to 2nd row:
Multiply 3rd row by -1 and add to 1st row:
Multiply 2nd row by -1 and add to 1st row:
Therefore, the inverse matrix is:
We can verify that:
*** END ***